Recently, there has been increasing interest in quantum materials, such as topological insulators, Dirac and Weyl semimetals, and beyond. These materials are characterized by non-trivial fermionic excitations and topologically protected electronic states, resulting in novel transport properties.
Our research efforts are focused on different aspects and properties of these materials. One direction is centered on the ability for the topological surface states to imprint their spin texture on adjacent magnetic layers, which is important for spin-charge conversion. We have been studying the spin-momentum locking of the surface states of a wide range of transition metals deposited on top of Bi2Se3 topological insulators using first-principles calculations.
Another direction in our research is focused of non-centrosymmetric materials, where spin-orbit coupling locks the electron’s spin direction to its momentum resulting in non-trivial spin textures in the reciprocal space. Depending on the crystal symmetry, the spin texture may exhibit Rashba, Dresselhaus, persistent, or more intricate configurations. In ferroelectric materials these spin textures are coupled to the ferroelectric polarization and thus can be controlled by its orientation and magnitude. This provides a promising platform to explore the coupling between spin, orbital, valley, and lattice degrees of freedoms in solids and opens a new direction for nonvolatile spintronic devices.
Quantum materials are also interesting for topological antiferromagnetic spintronics, where the Néel vector is used to electrically manipulate the symmetry of the related topological states. Based on density-functional theory calculations, we have demonstrated that room temperature antiferromagnetic metal MnPd2 allows the electrical control of the Dirac nodal line by the Néel spin-orbit torque. The reorientation of the Néel vector leads to switching between the symmetry-protected degenerate state and the gapped state associated with the dispersive Dirac nodal line at the Fermi energy.
References
- L. L. Tao and Evgeny Y. Tsymbal, Topical Review: “Perspectives of spin-textured ferroelectrics,” Journal of Physics D: Applied Physics 54, 113001 (2021).
- S. Laref, S. Ghosh, E. Y. Tsymbal, and A. Manchon, “Induced spin-textures at 3d transition metals/topological insulator interfaces,” Physical Review B – Rapid Communications 101, 220410 (R) (2020).
- D.-F. Shao, G. Gurung, S.-H. Zhang, and E. Y. Tsymbal, “Dirac nodal line metal for topological antiferromagnetic spintronics,” Physical Review Letters 122, 077203 (2019).
- L. L. Tao and Evgeny Y. Tsymbal, "Persistent spin texture enforced by symmetry," Nature Communications 9, 2763 (2018); Editor’s monthly highlight.
- D.-F. Shao, S.-H. Zhang, X. Dang, and E. Y. Tsymbal, “Tunable two-dimensional Dirac nodal nets in non-symmorphic compounds,” Physical Review B – Rapid Communications 98, 161104(R) (2018).
- L. L. Tao and E. Y. Tsymbal, “Two-dimensional type-II Dirac fermions in a LaAlO3/LaNiO3/LaAlO3 quantum well,” Physical Review B – Rapid Communications 98, 121102(R) (2018).
- C. X. Quintela, N. Campbell, D. F. Shao, J. Irwin, L. Xie, D. T. Harris, T. J. Anderson, N. Reiser, X. Q. Pan, E. Y. Tsymbal, M. S. Rzchowski, and C. B. Eom, “Epitaxial thin films of Dirac semimetal antiperovskite Cu3PdN,” APL Materials 5, 096103 (2017); Editor’s pick.
- L. L. Tao, T. R. Paudel, A. A. Kovalev, and E. Y. Tsymbal, “Reversible spin texture in ferroelectric HfO2,” Physical Review B 95, 245141 (2017).
- J. Zhang, J. P. Velev, X. Dang, and E. Y. Tsymbal, “Band structure and spin texture of the Bi2Se3/3d ferromagnetic metal interface,” Physical Review B 94, 014435 (2016).
- J. Betancourt, S. Li, X. Dang, J. D. Burton, E. Y. Tsymbal, and J. P. Velev, “Complex band structure of the topological insulator Bi2Se3,” Journal of Physics: Condensed Matter 28, 395501 (2016).
- X. Dang, J. D. Burton, and E. Y. Tsymbal, “Local currents in a two dimensional topological insulator,” Journal of Physics: Condensed Matter 27, 505301 (2015).
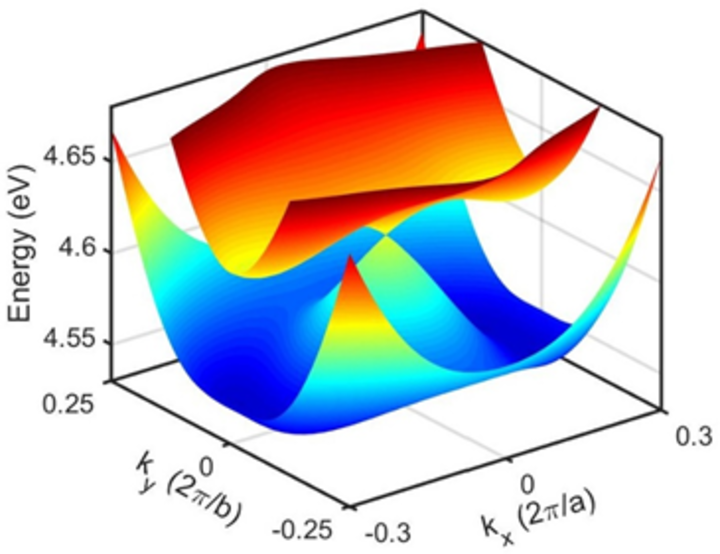
Predicted 3D Dirac point in te conduction band of ferroelectric HfO2.
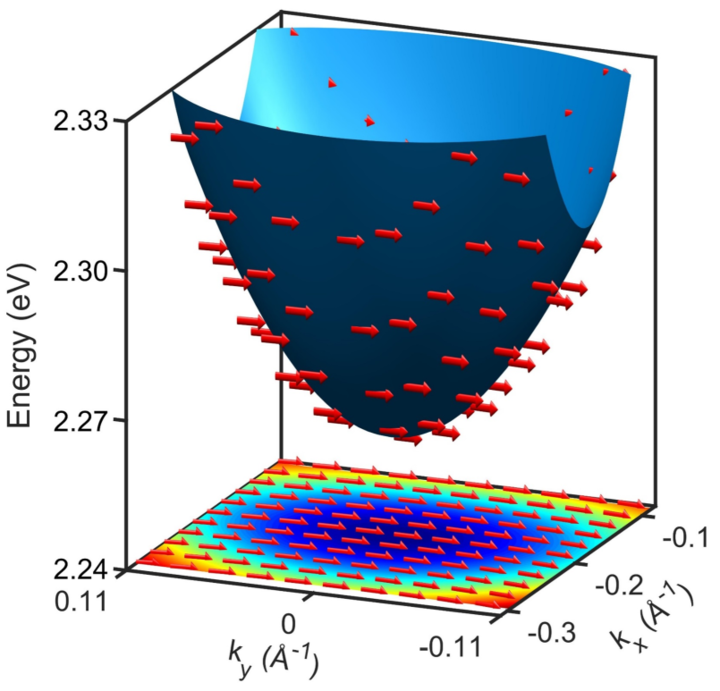
Persistent spin texture around the conduction band minimum of BiInO3.
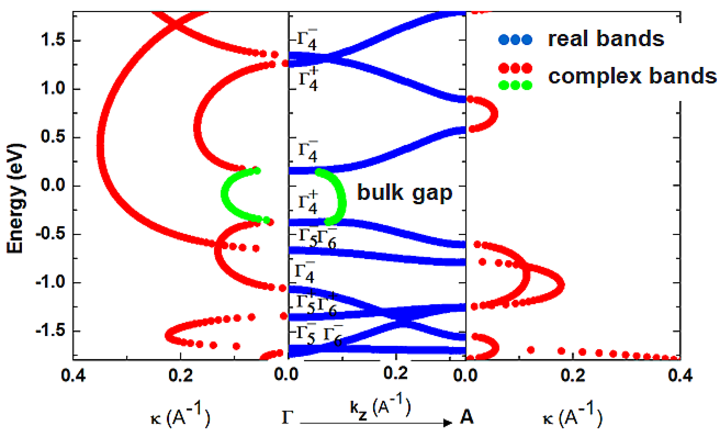
Complex band structure of Bi2Se3.